Algorithm
Learn More About Booth's Multiplication Algorithm
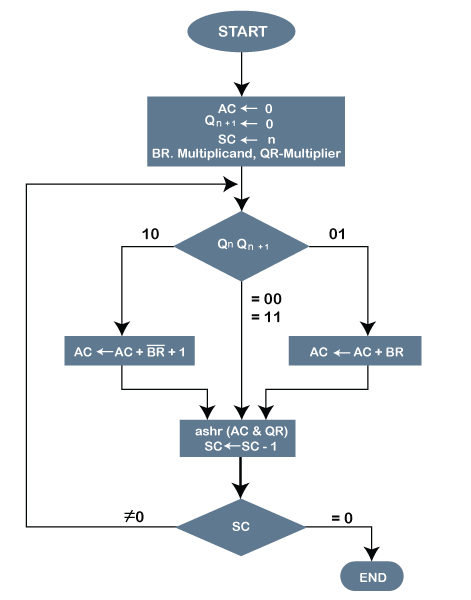
Booth algorithm gives a procedure for multiplying binary integers in signed 2's complement representation in efficient way, i.e., less number of additions/subtractions required. It operates on the fact that strings of 0's in the multiplier require no addition but just shifting and a string of 1's in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^(k+1 ) to 2^m. As in all multiplication schemes, booth algorithm requires examination of the multiplier bits and shifting of the partial product. Prior to the shifting, the multiplicand may be added to the partial product, subtracted from the partial product, or left unchanged according to following rules:
- The multiplicand is subtracted from the partial product upon encountering the first least significant 1 in a string of 1's in the multiplier
- The multiplicand is added to the partial product upon encountering the first 0 (provided that there was a previous '1') in a string of 0's in the multiplier.
- The partial product does not change when the multiplier bit is identical to the previous multiplier bit.
AC and the appended bit Qn+1 are initially cleared to 0 and the sequence SC is set to a number n equal to the number of bits in the multiplier. The two bits of the multiplier in Qn and Qn+1are inspected. If the two bits are equal to 10, it means that the first 1 in a string has been encountered. This requires subtraction of the multiplicand from the partial product in AC. If the 2 bits are equal to 01, it means that the first 0 in a string of 0's has been encountered. This requires the addition of the multiplicand to the partial product in AC. When the two bits are equal, the partial product does not change. An overflow cannot occur because the addition and subtraction of the multiplicand follow each other. As a consequence, the 2 numbers that are added always have a opposite signs, a condition that excludes an overflow. The next step is to shift right the partial product and the multiplier (including Qn+1). This is an arithmetic shift right (ashr) operation which AC and QR to the right and leaves the sign bit in AC unchanged. The sequence counter is decremented and the computational loop is repeated n times. Product of negative numbers is important, while multiplying negative numbers we need to find 2's complement of the number to change its sign, because it's easier to add instead of performing binary subtraction. product of two negative number is demonstrated below along with 2's complement.